human and environment
4-3. データの解析と評価
- ヒトからみた環境 - 玉利 祐三
- 4-3-1. 文献の意味するもの
- 作図の表現と解釈
母乳哺育の方が人工乳哺育よりも乳児のアトピー性皮膚炎の発症率が高く、これは母乳に含まれるダイオキシンによるものとされる説(民間非営利組織NPO、九州大学医療短期大学部長山淳哉監修、「ダイオキシン汚染列島・日本への警告」、かんき出版、1997、21頁)が定着し、このため母乳哺育での問題として、これがしばしば引用されてきました。下図は、 NPO「ダイオキシン問題を考える会」が作成したもので、書籍・解説書等にこの図がよく引用されています。この図は、「母乳の子に多いアトピー性疾患」と題して1997年10月14日の毎日新聞にも掲載されました。
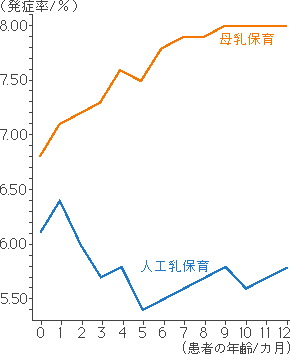
図5 図作成:ダイオキシン問題を考える会
原資料:厚生省児童家庭局
平成4年度アトピー性皮膚炎実体調査報告書
しかし、1999年5月27日の読売新聞では、「母乳中のダイオキシン説に異議」と題され、この図は、母乳哺育と人工乳哺育とにおける発症率の差を強調しすぎたものであることを、監修した九州大学医療短期大学部長山淳哉助教授が認めたとの記事が記載されました。
では、どうしてこのような図が作成されるに至ったのかを考察してみましょう。図6は、母乳哺育(図中の上側のライン)と人工乳哺育(図中の下側のライン)でのアトーピー性皮膚炎の発症率のデータをパソコンで処理、つまりクリケットグラフというソフトで処理した原図であり、作成者の意図なしに、パソコンのディスプレー上に直ちに作図されてくるものです。
そもそもデータをパソコン処理すれば、人が手作業でグラフを作図するよりも間違いがないと信じられているかもしれませんが、図6はまさに今回の問題の図そのものです。パソコンで処理した人も、それがプリンターで打ち出されてきた図を見た人も、母乳哺育と人工乳哺育で差があると判断してしまい、パソコンでデータ処理したのだから正しいと思いこみ、そのことに何の疑問も抱かないことでしょう。 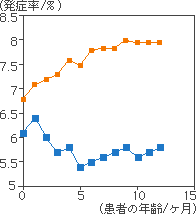
図6 パソコン(クリケットグラフ)で処理した原画
逆に、母乳哺育と人工乳哺育の差を意図的に強調したければ、図7のように縦軸を横軸よりも長くすれば、一層この差が強調できます。図の縦横比を逆にすると図8となり、図7とは多少趣が異なります。
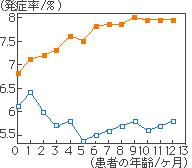
図7 発症率の差を強調した図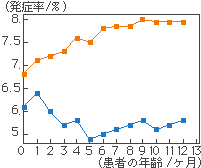
図8 図6の縦横比を変えた図
しかし、冷静かつ客観的にデータを見定め、ここで縦軸の発症率について零を原点とする図とするのが妥当と考えると図9となります。発症率を最大値の100%まで示しこれを縦軸にすれば図10となりますし、図10では明らかに母乳哺育と人工乳哺育の差は認められなくなることが分かると思います。
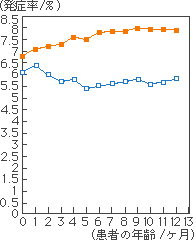
図9 図6の縦軸を零とした図
図10 図8の縦軸を最大100%とした図
これらの図の作成は、すべてパソコン上で入力項目を多少変更することで可能であり、初心者でも簡単かつ迅速に処理できます。しかし、図をどのように作図して見せるのか、発表するのか、データの妥当性、それまでのデータとの関連性、矛盾点など考慮したうえで作図表現(プレゼンテーション)するかは論文発表者(専門家)の責任でしょう。
一般的に、大学・研究所等では、データをパソコン処理することは日常的であり、教授は学生・院生等に指示することが多く、自らデータ処理する教授は非常に少ないと考えられます。教授は、学生のパソコン処理したフロッピーディスク(インストールされた作図)を受け取ることでしょう。だからこそ、教授はこの図の問題点を見抜くだけの素養が必要なのです。
また、今回のこの図ですが、これを他者(専門家、教授、助教授など)がしばしば引用していますが、同様のことが言えます。ともかく引用すれば「自分の責任はない、作成していないのだから」では通用しません。この問題の図(あるいはその内容)を引用しているものを、これまでの出版物約40冊について調査しました(巻末の参考資料参照)。その結果、約2割が引用していることが分かりました。データを引用することは容易なことですが、それを使って「お話し」ができ、一冊の「本」が出版されることも事実です。
以上のようにデータとは、如何ようにも表現できるものであり、結論・推論は変わり得ることがお分かり頂けたことと思います。「実際のデータであるから嘘ではない」、「だから正しい」と如何にも論理的ですが、それは、「100%正しい」とは限らないのです。データが全て100%正しいとは限らないことを理解してください。データの解釈・評価はただ一つのみではなく、別の見方もでき得ることを。
それでは、どのように作図表現すればより誤解が少ないのでしょう。それは、今回の各測定データについて、例えば母乳哺育の母親の各年齢で、2、3人のデータではなく少なくとも数十人のデータの平均値と標準偏差を合わせて図示すれば、このような今回の問題は起きなかったものと思います。例えば図11は、母乳中の必須ミネラルであるセレンの含有量を分娩後の経過日数による変化を示したものです(筆者ら、J. Trace Elements Med. Biol. 誌、9巻, 34-39, 1995掲載)。 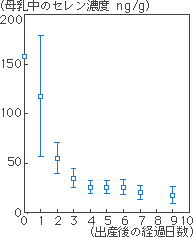
図11 母乳セレンの濃度変化
原資料:J. Trace Elem. Med. Biol., Vol.9,
1995掲載
このように、単なる平均値ではなく、その平均値に伴う標準偏差で示し、しかもその標準偏差が測定試料数に応じた、すなわち有意水準p、換言すれば危険率(図7では危険率1%)で示すほうが、その平均値の示す範囲、幅を理解することができ、より正確に命題を解析、つまりこの場合は、母乳セレン含有量が分娩後の経過月数と共に減少することが理解できるのです。
相関図の解釈と評価
もう一つの例は、これもよく見かける図があります。それは、例えば「血液中のある成分が増えると、ある発症率が大きくなる(あるいは、この症状に関したあるパラメーターの数値が大きくなる)。」という、いわゆる"相関関係"です。これは、実験(調査)データから作成されていますし、確かに学術論文にも掲載されているので、"間違いはない結論"です。しかし、"間違いはない"のではなくて、"別の考え方"、つまり"別の結論"も正しい場合があります。これは、「相関」、「有意水準」、「危険率」等で説明することができます。

図12 相関がある(相関係数0.602, p<0.05)
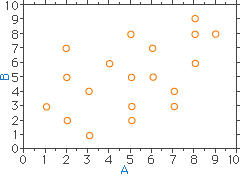
図13 相関がある(相関係数0.602, p<0.01)
- 例えば、図12(上側)で、相関係数rを算出するとr=0.65となることから、「A成分が増大すると、発症率Bは大きくなる」と結論づけられます。しかし、同じデータであっても、ある有意水準(例えばp<0.01、つまり危険率1%)で検定すると、「A成分が増大しても、発症率Bは変化しない(AとBには強い相関がみられない)」となることがあります(下側、図13)。
これが、動物実験という実験例の少ないデータから作図されていたとすると、もう一つの実験データが図にワンポイント追加されるだけで、算出される相関係数は大きく変動し、そのため結論がその一つのデータに大きく左右されることがあります。それが"相関図"の解釈であることを理解して下さい。
問題は、検定によっては「AとBに相関あり」とすることも正しいし、「AとBには相関がみられない」とすることも正しい場合があります。一方的な結論のみを信用することは非常に危険です。