human and environment

4-3. データの解析と評価

- ヒトからみた環境 - 　玉利祐三

4-3-2. 平均値と標準偏差: 　ある事柄について、いくつかの測定値があるとき、それを一つの代表値として示すことが多くあります。よく使用されるものとして、平均値（正しくは算術平均値ですが、略して平均値）、その他に幾何平均値、中央値などがあります。平均値は、測定値の全部を頻度分布（ヒストグラム）に作成したとき、左右対称の分布（正規分布、図14参照）を示す場合に算出が可能であり、それが左右非対象な対数正規分布を示せば幾何平均値で算出することになるし、最小値、最高値が特にかけ離れている場合には、中央値が用いられることになります。このように数値の集団を代表するには、その集団の内容にみあった表現としての"代表値"を選定しなければなりません。

　例えば、あるクラスで理科のテストを行ったとき、０点から100点（図の横軸）までの人数を集計（図の縦軸）して図に示したものが図8の得点分布（ヒストグラム）です。図14のようにこのクラス（母集団）の理科の平均値は計算すると50点であることがわかります。しかし、50点が平均といっても、図14のように０点から100点までまんべんなく分布しているのか、図15のように50点という平均点に集中しているのかでは意味が異なります。

　つまり、得点のバラツキを数値で示し、その範囲を明示すればよく理解できるはずです。だから、平均値に伴うバラツキの程度を標準偏差（SD: Standard Deviation）で示し、「平均値±標準偏差」として表すことが多いのです。例えば、図14では50±16点、図15では50±3点となるわけです。

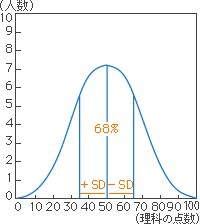図14　理科の得点分布

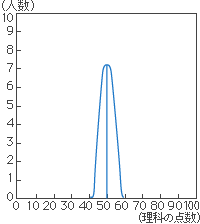図15　理科の得点分布

　このように理科の平均点（50±16点）と、例えば国語の平均点が25点であれば、両者を平均点で比較することは容易なのですが、国語が25±25点であれば、平均点として"国語（25点）の２倍が理科（50点）です"と表現できるのですが、理科では24～66点、国語は0～50点であり、内容的には両者にあまり差が見られません。

　従って、ある平均値と他の平均値を比較するとき「・・・の何倍・・・」と表現された数値の解釈は、以上の点をふまえて特に注意しなければなりません。

　「平均値±標準偏差」の範囲は、正規分布（のヒストグラム）で全体の68.3％での信頼区間の表示であり、信頼区間95.4％であれば「平均値±2×標準偏差」、99.7％であれば「平均値±3×標準偏差」、ちなみに95％であれば「平均値±1.96×標準偏差」と表します。

　しかし、一般的に学術論文などでは「平均値±標準偏差」で示されていることが多いのです。前述の理科と国語の例で、信頼区間99.7％とすれば、理科は50±48点（2～98点）、国語は25±75点（0～100点）となり、両者にほとんど差がないことがお分かりいただけると思います。しかし、平均値で言えば、理科は国語の"２倍"なのです。

　一方、栄養、公衆衛生学、医学等の専門分野では、後述するように仮説検定で有意水準（危険率）が用いられ、危険率５％（p＜0.05）と１％（p＜0.01）がよく用いられます。その場合、正しい仮説を捨ててしまう危険は、 p＜0.05よりもp＜0.01の方が少ないことは明らかです。

　前述の平均値を求めるとき、どの程度の信頼度、換言すれば平均値がどれくらいのバラツキの範囲を有するかは標本の数（試料数）により定まり、結論の誤りの確率（危険率、有意水準、信頼区間、信頼限界）で示すことは可能となります。

　従って、平均値に伴って算出される標準偏差は試料数によっても異なり、より正確な議論のためには、単なる標準偏差ではなく、ある有意水準にもとづく標準偏差を算出するほうがよいと考えられます。