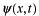
簡単のために、一次元空間を運動している粒子を考えます。その状態が波動関数 で表わされているとします。これは、あとでわかるようにシュレーディンガー方程式を数学的に解けば、その関数形を知ることができます。
重要なことは
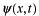
(1)は一般的には複素関数である。
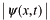
(2)関数は粒子が存在すると考えられる所で大きな値をとる。


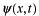
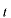
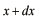
波動関数で記述される粒子が時刻、位置との間に観測される確率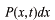は、


確率を全座標空間について積分すると定義から1ですから


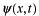
となります。つまり、は無限遠方で大きな値をとることが出来ないことを意味しています。ここでは、このような性質だけを頭に入れておきましょう。