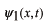
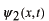
,がともにシュレーディンガー方程式の解であるとすると、


これらの両辺を加え合わせて、

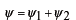
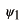
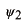
と書くことができて、もまたシュレーディンガー方程式の解になっていることがわかります。 このことを、「波の重ね合わせが可能である」といいます。詳しくは線形性、線形演算子のところで包括的に学習します。 ,は波動関数ですから、振幅と位相を使って表現できます。


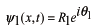
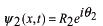
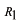
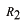
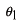
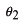
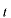
,はそれぞれの振幅、,は位相です。これらはすべてとの関数ですが、ここでは省いています。

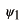
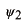
との波を重ね合わせてできる波はどんな振舞いをするでしょうか？



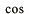
左辺の第3項は関数で、位相に依存して振動する項です。これを干渉項といいます。

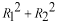
単にになっていないことに注意してください。

量子力学では2つの状態が重ね合わされると干渉を生じます。この式はそのことを表わしています。