波動関数は時間的に変化する波ですから、それによって表現されている粒子が時間的にどのように運動しているのかを対応づけることは困難です。すこしでもそのことをイメージアップするために、確率の流れを考えてみましょう。

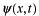
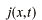
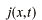
　教科書には波動関数から、確率の流れに対応する流束をどのように導くかが書かれています。流束はで表わされます。三次元になると、これはベクトル量になります。の導きは簡単ですから各自チェックしておいて下さい。

流束は次のように表わされています。


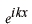
　これを平面波に応用してみましょう。コンプトン散乱のときに、池の真中に立てられた棒に入射する平面波のことを考えました。そのとき波は棒に向かって進んでくると表現しました。

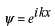
として流束を計算してみましょう。


であることを忘れないようにして下さい。


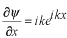
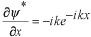
ですから、これらを定義の式に代入して


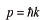
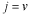
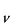
となります。の関係を思い起こすと、となり、の速さで軸の正の方向に流れている感じを理解して下さい。

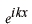
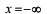
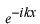
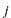
　第5章でポテンシャルの問題を解くとき、軸の方向に進む自由粒子の波動関数を平面波で表わします。これを内向波と呼ぶこともあります。それは、から原点に向かってくる波だからです。 平面波についても同じことを行ってください。の値はいくらになりますか？