或る物理的な状態、例えば粒子が運動量
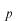
をもって自由に運動している状態は
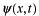
で表わされます。この状態のもとで、

の関数
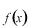
の期待値を計算することができます。
期待値は
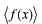
と書きます。確率密度
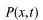
を用いて
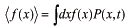
−−−(a)
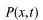
は
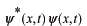
で表わされますから
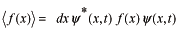
−−−(b)
ここで、
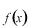
を
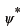
と
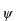
でサンドイッチにします。この様に表現しますと、
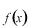
は単なる関数ではなく、演算子という意味を持たせていることになります。
(a)から(b)への移行には説明しなければならないことがあるのですが、ここでは(a)は関数
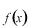
の重み関数
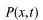
による平均という我々になじみのある考え方であり、(b)は演算子
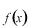
の状態
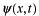
での期待値という量子力学的な扱いであることに注意するだけにしておいて下さい。
(b)場合、むやみに
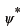
,
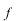
,
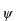
の順序を変えることができないのです。このことは次第に理解できてきます。
次に
運動量の期待値を考えることにしましょう。
ですから
先程の定義により
ですから
となります。ここで、時間とともに変化するのは
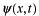
と
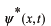
だけですから、積分の中に
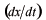
は現れません。
時間に依存するシュレーディンガー方程式は
で、両辺を
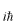
で割ってみると
これの複素共役をとると
これらを先程の
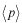
の式の右辺に代入して計算すると、
となることはわかるでしょう。
この被積分関数を少し変形しましょう。目的は積分できるところは積分を実行してしまおうということです。何にも具体的に
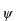
の関数の形がわかっていないのにどうして積分が出来るのか不思議に思うかも知れません。ここでは
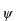
や
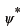
は
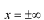
で0になっているという性質を使います。この性質は全確率が1になるために必要な条件であったことを思い起こして下さい。
先ず、
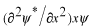
は
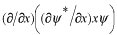
という項にくらべて、どれだけ余分の項を含んでいるか考えます。そのためには実際に
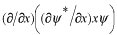
を3つの合成関数の微分として、微分を実行すればよくわかります。結果は
となります。同じことを
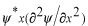
の項についても考えてみます。
となります。もう一つ、
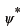
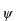
の微分を考えておきます。
これら三つの関係式から教科書に書かれている
が被積分関数の
に対応していることがわかると思います。
それでは積分を実行します。
この値をどのように評価すればよいか考えてみましょう。この様な積分評価は量子力学の式の操作にはよく出てきますのでコツを会得しておいて下さい。先程も述べたように、
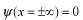
と考えて、この積分値は0になります。
従って、
最後の行に移るときに、2が分母分子にあるので打ち消して、
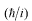
の場所を移動させました。
期待値の定義に従って
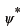
と
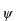
ではさまれているものが、演算子ですから、運動量
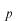
の演算子は
と表わされていることがわかります。
演算子はoperatorですから、
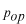
のように添字で演算子であることを明記します。この他に
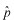
のように山形の記号を用いて演算子であることを表現する場合もあります。
量子力学では演算子とそうでないものを意識して式を見ていかなければなりません。