時間に依存しない物理的な状態、これを定常状態といいます。時間とともに、その形がかわらない波です。この時間に依存しない状態を、波動関数で
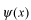
と表わすとき、座標表示を使っているといいます。つまり、
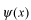
は
座標空間での波動関数です。
それでは、
運動量空間での波動関数はどのように表わされるのでしょうか。ここで、状態をどの空間での波動関数として表わすのかは自由です。考えている問題に応じて、都合のいい表示を用います。表示が違っても状態そのものが変わるわけではありません。
この章のはじめにでてきた
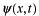
と
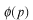
の関係式で
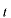
=0とおいて
という式が得られます。
フーリエ積分の逆公式を用いると
となります。
ここで
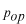
の期待値が
と表現されるのであれば、
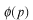
は運動量空間での波動関数と解釈されます。それを確かめてみましょう。
まず、
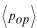
は次のように書けました。
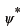
と
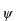
で演算子
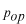
をサンドイッチにして積分するというのが期待値を求める方法でした。右辺は

空間で表示されていますから、これを
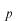
空間での表示に変えていきます。まず、右端の

を
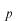
空間の波動関数に変換します。
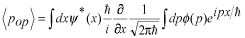
(微分を先に実行します。)
(次に
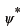
を
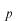
空間の波動関数に変換しますが
積分変数は
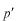
とします。すでに
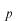
は一度、使っています。)
ここで、
を使っています。
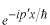
のように負の記号がついていることに注意して下さい。
何故かわからない人は、もう一度、複素共役の所を勉強して下さい。
整理すると、
ここで
を使います。
すると、
これを
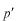
について積分を実行します。
最後のところで
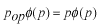
という関係式を使いました。
これは演算子
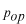
の固有値方程式で、次の章で勉強します。
このとき、
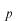
を固有値と言います。
この段階では深く理解しなくてもよろしい。
ただ、
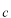
-数である
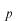
の位置は自由に変えることはできますが、演算子
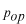
は
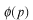
に作用するため、位置が決まっていることだけに注意しておいて下さい。