| 戻る |
|
|
quantum mechanics
4-5. ポテンシャルに束縛された粒子の
固有値問題 - 二階線形常微分方程式の解法 - 量子力学 - 太田 雅久
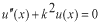 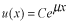 と仮定してみます。このように仮定する理由は、この種の方程式が と仮定してみます。このように仮定する理由は、この種の方程式が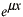 の形の解を持つことが知られているからです。これを微分方程式に代入します。 の形の解を持つことが知られているからです。これを微分方程式に代入します。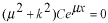 この式が成り立つためには 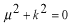 を 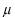 が満たさなければなりません。この式のことを特性方程式といいます。この場合は が満たさなければなりません。この式のことを特性方程式といいます。この場合は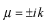 という2根を持つので、解は 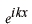 , , 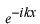 となります。 一般に 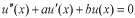 の場合も同様に特性方程式は 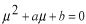 この2根を 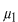 , ,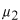 とすると、独立な解は とすると、独立な解は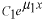 , , 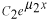 となります。 重根の場合は自分で数学の本を調べてみてください。 |
|