無限に深い井戸型ポテンシャルに閉じ込められている粒子のエネルギー準位を求めてみよう。これは
ハミルトニアン
の
固有値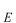
を求める
固有値問題です。
無限に深いポテンシャルの幅を
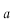
として、このポテンシャルの様子は次のように数式で表現されます。
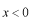
及び
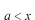
の区間ではポテンシャルが無限大であり、粒子が存在する余地がありません。従って、粒子の確率振幅である波動関数はゼロとなります。このポテンシャルの場合は、
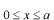
の区間のみ

を考えればよろしい。
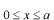
の区間でハミルトニアンを考えてください。
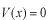
ですから
となります。求める波動関数を
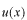
として、固有値方程式
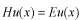
を具体的に書くと、
この微分方程式の解法の技法の一つとして、両辺を
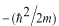
で割って形を整えます。
この種のシュレディンガー方程式を解く場合に、係数
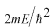
に注目します。うまい具合に、この量は
波数に対応しています。
そこで
とおきます。固有値
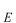
を求めるということが、波数
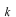
の値を求めることにかわります。方程式を書き換えてみます。
これは
二階の線形常微分方程式です。
シュレディンガー方程式が、いつもこのような簡単な方程式になるとは限りません。ポテンシャルが
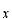
によらず、定数(ここではゼロ)であったからです。
この方程式の独立な解は
です。
この方程式の一般解は、この二つの独立な解の重ね合わせとなります。
さて、この波動関数に対する境界条件はどうなっているでしょうか。
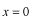
と
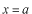
で波動関数がゼロになっています。このことを使って、
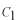
,
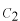
及び
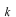
を決めます。
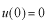
より
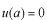
より
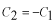
であることを用いて、
この式が成り立つためには
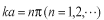
でなければなりません。
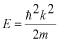
の関係を思い出してください。
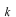
の値が決まったわけですので、固有値
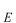
が決まったことになります。
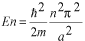
,
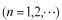
次に、波動関数(この場合は
固有関数と呼んだ方がいいかもしれません)は
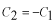
より
ここで、この
関数を規格化します。つまり、
となるように
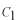
の値で決めます。
ですから
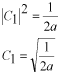
(
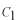
を実数と仮定して)
従って、規格化された波動関数は
となります。ここで計算の過程で
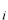
が出てきましたが、
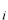
は絶対値が1で位相のみに関係する因子です。前にも言いましたように、位相まで決定することはできません。従って、普通は
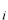
を取り除いて
が規格化された波動関数(固有関数)として扱われます。
明らかに、
が成り立ちますので、異なる固有値に対応する固有関数は
直交しています。