今問題にしていたポテンシャルは
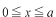
の区間に井戸の底がありました。
これを

の負の方向に
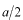
だけ移動させます。
物理的には状況は変わりません。数学的には井戸の定義区間が
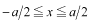
となり、

軸に対して対称なポテンシャルになります。
ポテンシャルが
空間対称性を持つと、波動関数は対称性によって分類されることになります。
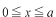 | ・・・ |
原点で0の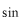 関数(奇関数のみ) 関数(奇関数のみ) |
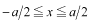 | ・・・ |
原点で0の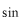 関数 関数
原点で0でない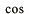 関数(偶関数と奇関数) 関数(偶関数と奇関数) |
波動関数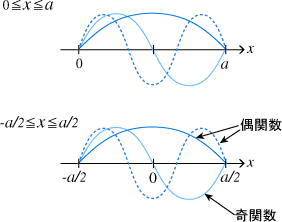
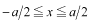
の区間にポテンシャルを定義すると、波動関数に
偶関数と
奇関数が混ざってきます。
波動関数は
対象ポテンシャルでの波動関数の求め方は各自で試みてください。解答例は[基礎知識アペンディクス:対象ポテンシャルでの解法]を参照してください。波動関数の偶奇性はあとで重要になります。