| 4-6 |
| 5-1 |
|
|
|
quantum mechanics
4-7. 展開仮定とその物理的意味
量子力学 - 太田 雅久
深い井戸型ポテンシャルに束縛された粒子の固有関数の組
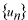 で、同じ境界条件 で、同じ境界条件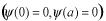 を満たす任意の関数を展開することが出来ます。これはフーリエ級数展開と同じです。 を満たす任意の関数を展開することが出来ます。これはフーリエ級数展開と同じです。
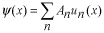 係数 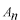 の求め方は、上式の両辺に左から の求め方は、上式の両辺に左から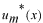 と掛けて、定義区間である と掛けて、定義区間である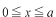 で積分します。このとき、直行関係式を用います。 で積分します。このとき、直行関係式を用います。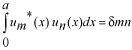 右辺はクロネッカーのデルタといいます。 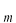 と と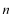 の値が等しいときに1を与えます。その他は0です。従って の値が等しいときに1を与えます。その他は0です。従って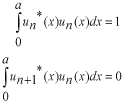 この関係式を用いると、 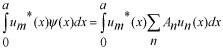 ここで 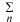 は積分記号の左に出してもよろしい。また は積分記号の左に出してもよろしい。また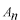 は変数 は変数 に関係しませんから積分の外に出します。 に関係しませんから積分の外に出します。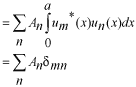 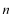 は1から2、3、・・・と変わってゆきますが、 は1から2、3、・・・と変わってゆきますが、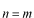 になったとき、 になったとき、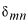 は1となりますので、その時だけ値が残ります。 は1となりますので、その時だけ値が残ります。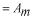 従って、 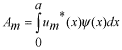 通常、 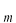 の代わりに の代わりに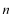 を使って を使って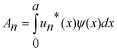 と書きかえます。 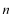 の記号が一般的に使われるというだけの理由です。 の記号が一般的に使われるというだけの理由です。係数 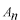 の物理的意味は、もし、任意の状態 の物理的意味は、もし、任意の状態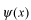 でエネルギー でエネルギー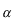 の期待値を求めると、 の期待値を求めると、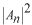 の確率でエネルギー期待値 の確率でエネルギー期待値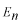 が出現するということになります。 が出現するということになります。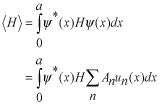 ここで 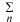 と係数 と係数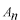 を積分の外に出し、 を積分の外に出し、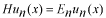 という固有値方程式を用いて、演算子  を固有値にかえます。演算子 を固有値にかえます。演算子 は一般的には右側にある関数に作用します。 は一般的には右側にある関数に作用します。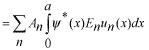 ここで、先程 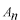 を求めた式を思い出します。ただし、様子が少し違います。 を求めた式を思い出します。ただし、様子が少し違います。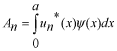 でしたが、今度は、この式全体の転置共役をとったものが必要になってきます。 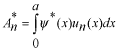 関数の順番も転置しています。 この式を用いますと、 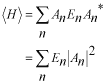 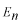 の期待値が現れる確率は の期待値が現れる確率は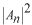 となります。 となります。
|
|
|