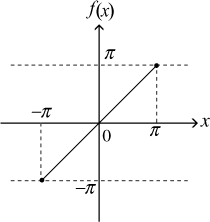
典型的なフーリエ級数展開を思い出しましょう。
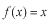
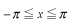
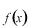
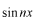
をの区間でフーリエ級数展開してみましょう。は奇関数ですから奇関数であるで展開すれば充分です。


従って、



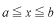
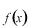
一般に区間でののフーリエ展開は


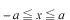
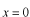
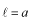
無限に深い井戸型ポテンシャル中の粒子の波動関数はの区間でポテンシャル問題を考え、で波動関数がゼロとなる奇関数のみを考慮したと考えると、で


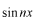
となります。任意の関数が固有関数で展開されるということと、フーリエ級数展開がここでは一致します。これは固有関数の組が、フーリエ級数展開の基本関数の組と一致しているからです。