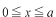で定義されたポテンシャルの場合と途中までは同じです。シュレディンガー方程式は


で、この方程式の独立な解は


と同じです。
異なる点は境界条件です。


に変更されます。
一般解は


です。これに境界条件を適用して、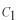,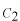,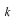を決めます。

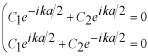---------(1) ---------(2)

(1)、(2)をそれぞれ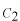について解くと、

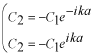---------(3) ---------(4)

となります。これは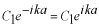つまり


でなければならないことを意味しています。つまり、


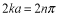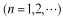
よって、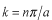となって、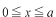の場合と同じ結果になります。
この結果を(3)又は(4)に適用しますと、


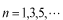のように奇数の場合は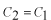

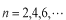のように偶数の場合は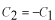
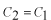の場合


となって偶関数の解となります。
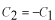の場合


となって奇関数の解となります。