固有値方程式を解く練習をしましょう。
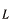
「演算子が


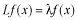
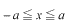
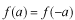
で与えられている。このとき、という固有値方程式をの区間で、という境界条件のもとで解きなさい。」
というのが典型的な問題の言いまわしです。

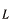
ここで区間がどのようになっていて、どんな境界条件であるのかをしっかりと認識しなければなりません。このケースでは、後は微分方程式を解くだけとなります。を具体的な形で示すと、方程式は


となります。


として両辺を積分すると、


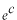
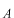
従って、をとおいて


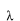
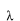
ここで気にとめることは、が決まっていないということです。このは境界条件により決まります。つまり、固有値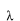は境界条件から決まるということです。


ですから、


つまり


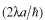
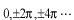
ということは、指数関数のベキにある位相部分が、ということになります。


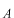
これで固有値(とびとびの値、つまり、離散的な値)が決まり、波動関数は定数因子を除いて決まりました。
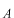
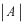
定数因子は通常は気にしませんが、規格化することによって一意的に決めることができます。しかしのみが決まるだけで、位相因子まで決めることはできません。