| 4-2 |
| 4-4 |
|
|
|
quantum mechanics
4-3. 線形演算子
量子力学 - 太田 雅久
私達が扱う固有値方程式に出てくる演算子は何であってもいいというわけではありません。私達がこれから使う演算子は、線形演算子という特別なものです。この演算子のもとでは「波動関数の重ね合わせや、定数倍した波動関数も元の演算子の固有関数である」と言われるようなことが可能になります。
線形演算子かそうでないかを識別する方法を述べます。具体的な例について自分で練習してみて下さい。線形演算子 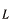 は次の2つの性質を満たすものとして定義されます。 は次の2つの性質を満たすものとして定義されます。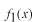 、 、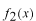 は任意の関数と考えてください。 は任意の関数と考えてください。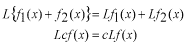 先ず最初、この関係式を見てあたりまえのことと思うかも知れません。しかし、もし演算子 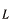 が次のような機能を持っている場合を考えてみましょう。 が次のような機能を持っている場合を考えてみましょう。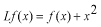 この式の読み方は演算子 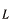 が任意の関数 が任意の関数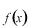 に作用するとその関数自身と に作用するとその関数自身と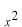 の項を作り出す、という様になります。さて、この演算子は先ほどの線形演算子の定義を満たしているでしょうか。
第一番目の式について考えてみます。 の項を作り出す、という様になります。さて、この演算子は先ほどの線形演算子の定義を満たしているでしょうか。
第一番目の式について考えてみます。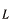 の機能から の機能から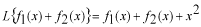 となります。また、右辺の各々の項は 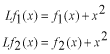 となり、明らかに 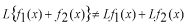 です。従って、この 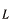 は線形演算子ではありません。 は線形演算子ではありません。次の演算子に関して、それらが線形かどうかを確かめて下さい。 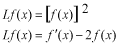 |
|
|