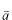
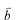
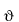
線形数学で習ったことを思い出してください。或るベクトルを別のベクトルに写像する演算子をと書くとします。この写像は式で表すと、


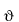
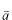
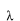
となります。もし、演算子がベクトルを倍するものであれば、この方程式は


となり、写像によって、方向は同じで大きさの異なるベクトルになるという関係を表しています。この種の方程式を固有値方程式といいます。

先ほど述べた時間に依存しないシュレディンガー方程式は固有関数になっているでしょうか。実は


はという記号で表されるハミルトニアン演算子として呼ばれるものなのです。を用いて先ほどの式を書き直すと


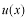
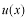
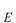
となります。は物理状態で、有限次元の場合はベクトルに対応するものです。演算子が状態に作用したとき、同じ状態だけれども倍だけ異なる状態になることを意味しています。即ち固有方程式になっています。