時間に依存するシュレディンガー方程式をもう一度見てみましょう。


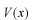
この偏微分方程式はポテンシャルが座標だけの関数で時間に関係しないために、ここでは変数分離できる性質を備えています。

先ず、この方程式の解が時間と座標だけの関数の積で表現できるとします。


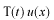
これを、上記のシュレディンガー方程式に代入して両辺をで割ると、


となります。必ず自分で確かめてください。

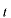
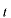
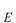
左辺はのみに、右辺はのみに関係する項から成り立っています。のいかなる値に対しても左辺と右辺が等しいということはこの両辺が定数(例えば)でなければなりません。
従って、


の二式が得られます。

最初の方程式は容易に解くことができます。この解き方は覚えておいて下さい。


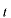
と変形して、この両辺を時刻0からまでの区間で積分します。


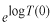
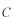
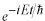
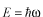
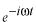
ここでを定数としました。或いはを用いると、がシュレディンガー方程式の時間変動部分です。

第二番目の式が、これからしばしば出てくる式で、正式には時間に依存しないシュレディンガー方程式と呼ばれているものです。この式は固有値方程式となっています。