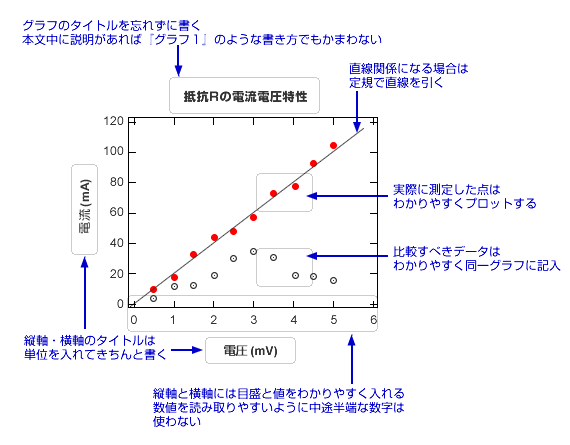 |
|
 |
その他
- グラフがあればデータ表は特別な場合を除き不要
- グラフは後で数値が読み取りやすいように書く
- プロットした
のところには数値は書かない。数値は軸に書く。 - どのような物理現象を表現したいかよく考えて、それが表現されるようにグラフを工夫する。
対数グラフを使うとき
下記の３パターンで左右のグラフは全く同じ点をプロットしたものである。左側が方眼グラフ、右側が対数グラフである。全く同じ点にもかかわらず、対数グラフの方が関数系が非常に見やすいことに注意して欲しい。
-
y = Aexp(Bx) である関数のとき
対数グラフでは直線になり、その傾きがBとなる。また接辺からAがもとまる。指数関数であることと傾きからBがすぐにわかる。方眼グラフではわからない。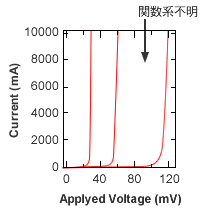
-
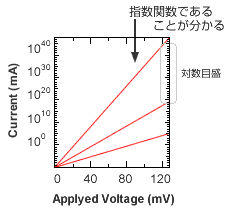
何桁も変わる現象をグラフ化するとき
横軸が何桁も変わる例。方眼グラフでは小さい値は読み取れない。対数グラフならどこにピークがあるかすぐにわかる。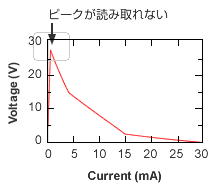
-
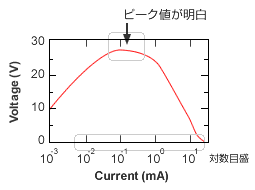
y = Axn のとき
両対数グラフを使えば直線となり傾きがnとなる。べき乗関数であることがすぐ分かる。方眼グラフではn=1のときのみ直線となる。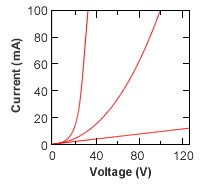
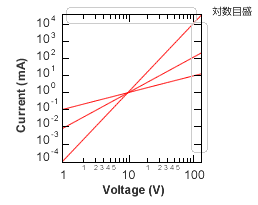
片対数グラフの傾きから関数y=Aexp(Bx) の定数A, Bを求める方法
片対数グラフにプロットする事は、方眼グラフでlog10yを縦軸にとることに等しい。
したがって
傾きの定義より傾きＳは
ショットキーダイオードの電流電圧特性は
q: 電子の電荷の絶対値
k: ボルツマン定数
T: 絶対温度（本実験の場合室温なので300Ｋとおく）
n: 理想係数
I0: 逆方向飽和電流
である。IとVを除いた記号のうちI0 とn以外は定数である。したがってグラフの傾きから上記の説明を利用して、理想係数n,y軸との切片から逆方向飽和電流I0 を求めることができる。
片対数グラフにプロットする事は、方眼グラフでlog10yを縦軸にとることに等しい。
したがって
log10y = log10(Aexp(Bx))
= log10A + B x log10e
= (B log10e) x + log10A
これはlog10yがｘに関する一次方程式の形をしていることを示す。したがって傾きが(Blog10e)ｘ=0でのｙ軸との切片がlog10Aとなる。対数グラフでの傾きは直線上の2点( x1 , y1 ),( x2 , y2 )を考えればすぐに求まる。= log10A + B x log10e
= (B log10e) x + log10A
傾きの定義より傾きＳは
S = ( log10y2 - log10y1 )/x2 - x1
である。したがって
B log10e = S
B = S/log10e
となり傾きが求まる。ショットキーダイオードの電流電圧特性は
I=I0exp(qV/nkT)
である。今実験でIとVの関係が求まった。この式でq: 電子の電荷の絶対値
k: ボルツマン定数
T: 絶対温度（本実験の場合室温なので300Ｋとおく）
n: 理想係数
I0: 逆方向飽和電流
である。IとVを除いた記号のうちI0 とn以外は定数である。したがってグラフの傾きから上記の説明を利用して、理想係数n,y軸との切片から逆方向飽和電流I0 を求めることができる。
Copyright(c)2004 Konan University All Rights Reserved.