| 7-6 |
| 原価計算 | 長坂悦敬 |
|
第7章 部門費の第1次集計
7-5 部門費の第2次集計 |
|
第1次集計では、各製造部門や各補助部門に部門費が集計されるが、それらは最終的に製品に負担せねばならない。しかし、補助部門費は、そのままでは製品に集計できない。そこで、製造部門に配賦する手続をとる。これが部門費の第2次集計(または補助部門費の製造部門への配賦)である(図表7-2)。そこでは、部門費配賦表(または部門費振替表ともいう)を用いて、補助部門に集計された部門費を一定の配賦基準と配賦法によって製造部門に配賦する。この手続によって全ての部門費が製造部門に集計される。
第2次集計では、補助部門費のサービスの利用の程度をよりよく反映できる適切な配賦方法が必要である。とりわけ、複数の補助部門が存在し、補助部門の間でサービスの授受を行っている場合、このサービスの授受をどのように扱うかが問題になる。補助部門間のサービスの授受を計算上どのように考慮するかによって、以下に説明する直接配賦法(direct distribution method)、階梯式配賦法(step-ladder method)および相互配賦法(reciprocal distribution method)という方法のいずれかが選択され、第2次集計が行われる。
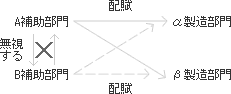
直接配賦法は、補助部門が他の補助部門にサービスを提供していたとしても、これを一切無視し、製造部門に対してのみサービスを提供したと仮定して補助部門費を製造部門のみに配賦する。
図表7-4 直接配賦法
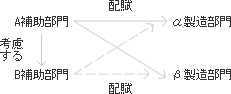
階梯式配賦法は、補助部門どうしのサービスの授受について、優先順位を決めて、その優先順位の高い補助部門から優先順位の低い補助部門へと一方向のみに配賦計算を行う方法である。自部門のサービス提供は無視し、サービスの提供を受ける他の補助部門を多く有する補助部門の優先順位が高くなるようにする。サービスの提供を受ける他の補助部門の数が同数である補助部門が複数存在するときは、その中で補助部門費の金額が大きい部門の優先順位が高くなる。
図表7-5 階梯式配賦法
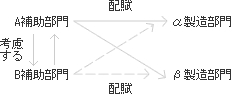
相互配賦法は、補助部門間のサービスを考慮する配賦計算法である。この方法では、部門間のサービス提供割合を考慮して配賦計算するので、より正確な計算を行うことができる。相互配賦法では、他部門に配賦すると同時に、他の補助部門から配賦を受ける。厳密に計算するならば、補助部門費がゼロになるまで配賦を繰り返すべきである。実際に使われている相互配賦法には簡便法、連続法、連立方程式法などがある。ここでは簡便法と連立方程式法を説明する。
図表7-6 相互配賦法法
簡便法は、以下のように第1次配賦と第2次配賦という2つの手続によって配賦を行う方法である。
1.第1次配賦
補助部門がサービスを提供した他のすべての部門に補助部門費を配賦する。ただし、自部門にサービスを提供していたとしても自部門には配賦しない。これにより、第1次集計によって各補助部門に集計された金額の全額が他の製造部門および補助部門に配賦される。
2.第2次配賦
第1次配賦によって、補助部門に他の補助部門から配賦額を受ける。第2次配賦では、各補助部門に集計された金額を製造部門に対してのみ配賦する。すなわち、直接配賦法による配賦を行う。
連立方程式法は、配賦計算をより正確に行うために、相互に配賦が行われる関係を連立方程式として定式化し、処理する方法である。最近の表計算ソフトウェアを用いれば比較的簡単に計算することができる。計算方法を以下に説明する。
まず、Xiを補助部門iの相互配賦後の原価とすると、それは次式のように表すことができる。
Xi = 配賦前の補助部門iの部門個別費 + 各補助部門から補助部門iへの配賦額 (7-1)
ここで、補助部門iに対する補助部門jからの配賦比率をaijとすると(7-1)式の右辺第2項は次式のように表される。ただし、自部門への配賦は行わないのでaii = 0である。
各補助部門から補助部門iへの配賦額 = Σnaij・Xi j = 1,n (7-2)
nは補助部門の数を示す。
また、製造部門kの配賦後の最終的な部門費Ykは次式のように表すことができる。
Yk = 配賦前の製造部門kの部門個別費+各補助部門から製造部門kへの配賦額 (7-7)
ここで、製造部門kに対する補助部門jからの配賦比率をbkjとすると、(7-7)式の右辺第2項は次式のようになる。
各補助部門から製造部門kへの配賦額 = Σn bkj・Xj j = 1,n (7-4)
さらに、配賦前の補助部門iの部門個別費をciとし、(7-1)式を行列式で表すと次のようになる。
X = c + a・X (7-5)
これは次のように変形できる。
X = (E - a)-1・c (7-6)
ただし、Eは単位行列である。したがって、この(E - a)-1という逆行列を求めればXiを計算することができる。Xiがわかれば(7-4)式が計算でき、最終的に(7-7)式からYkを求めることができる。
| 7-6 |