Lambertの法則 (溶質の長さと光吸収との関係)
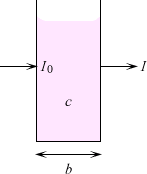
図2・6 光の吸収
(図2・6)のように、濃度(concentration)

の呈色溶液を液層の長さ
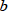
の容器(吸収セル)に入れ、これを単色光が透過したとき吸収が起こったとし、入射光束(incident beam)の強さを
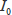
、透過光束(transmitted beam)の強さを

とします。いま、液層
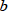
を同じ長さの仮想的な薄い層に分けて考えると、溶液が均一であれば光が透過したとき各層は同じ割合だけ光を吸収する(光の強さを減じる)と考えることができます。例えば、第1の層が入射光の1/2だけ吸収したとすれば、透過後ははじめの光の強さの1/2となり、第2層ではさらにその1/2を吸収し、はじめの光の強さの1/4になります。以下同様にして第3、第4、・・・の層を透過後は1/8、1/16・・・なります。これをグラフに画けば指数曲線となり、
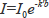
または
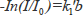
と表すことができるのです。以上のことを数学的に扱えば、次のようになります。単色光が媒質の中を通過するとき、光束に直角な長さ
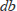
の薄層を考えると、
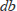
を通過後の光の強さの減少量
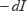
は

と
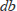
とに比例します。すなわち、
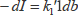
(2・3)
これを変形すれば、
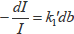
(2・3)
両辺をそれぞれ
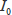
から

、0から
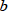
まで積分すれば、
常用対数に直せば、
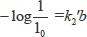
(2・4)
となり、透過光の強さは媒質の長さが増加するにつれて指数関数的に減少する事になります。
