MEKCは電気的に中性な分子を電気泳動により分離することを可能にした手法であり,界面活性剤ミセルをキャリアーとして用いるEKCをMEKCと呼んでいます。EKCのキャリアーとしてはミセルのほかに,イオン性官能基をもつシクロデキストリンやイオン性高分子,マイクロエマルジョンなどが利用されています。MEKCの装置はCZEのものと同じであり,泳動溶液にイオン性界面活性剤のミセル溶液を用いる点だけが異なります。もっともよく用いられる界面活性剤は陰イオン性のSDSであり,ここでは陰イオン界面活性剤を用いた場合を例として説明します。ミセルは負電荷を持つため,電気泳動により正極方向へ移動します。一方,溶液全体は電気浸透流により負極方向へ移動します。先に述べたように一般に電気浸透流速度はイオンの泳動速度よりも大きいため,ミセルは電気浸透流よりも遅い速度で負極方向に移動します。この系に電気的に中性な試料を導入すると,試料分子の一部はミセルに取り込まれ,取り込まれた試料分子はミセルとともに泳動します。一方,水相中に存在する分子は電気浸透流によって移動し,その速度は電気浸透流速度に等しい。ミセル相-水相間の分配平衡はミセルの泳動速度よりも十分速いので,ミセルに取り込まれる割合,すなわちミセルへの配分係数によって中性分子の泳動速度が決定されます。このとき,ミセルにまったく取り込まれない分子がもっとも速く泳動し,完全に取り込まれる分子がもっとも遅く泳動することになります。MEKC分離の模式図を図6・3に示します。
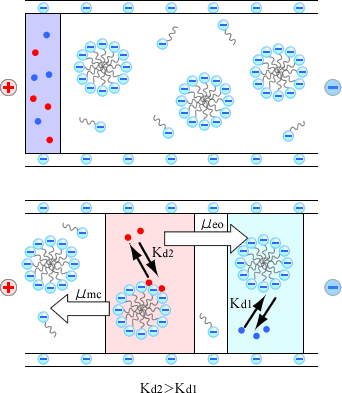
図6・3 MEKCの分離原理
電気浸透流速度を
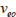
,ミセルの泳動速度を
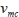
とすると試料分子のみかけの速度
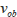
は次式で表されます。
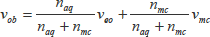
(6・10)
ここで
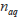
,
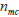
はそれぞれ水相中およびミセル相中に存在する溶質の総モル数です。クロマトグラフィーのパラメーターであるキャパシティーファクター
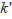
を,
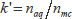
と定義すると式(6・10)は次のように書き換えられます。
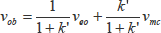
(6・11)
溶質の保持時間を
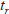
とすると式(6・11)より保持時間は次式で表されます。
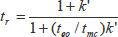
(6・12)
ここで
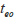
,
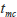
はそれぞれ電気浸透流およびミセルが検出器に到達するまでの時間であり,すべての中性分子は
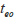
,
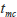
の間の時間に溶出します。
また は
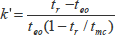
(6・13)
となります。実際のクロマトグラム上で横軸を保持時間と
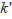
で表すと図6・4のようになります。
図6・4 キャパシティーファクター
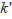
は分配係数
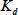
と次のような関係にあります。
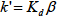
(6・14)
ここで
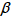
は水相とミセル相との体積比であり,
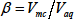
です。
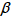
は界面活性剤の濃度
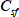
と臨界ミセル濃度
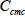
を用いて次のように表すことができます。
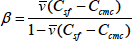
(6・15)
ここで
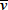
はミセルの部分比容と呼ばれる値であり,界面活性剤分子1モルが占められる体積で表されます。ミセル濃度が十分に低いときには式(6・15)の分母は1に近似できるので式(6・15)は次のように書けます。
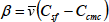
(6・16)
式(6・16)を式(6・14)に代入して次式を得ます。
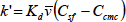
(6・17)
この式は
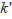
が界面活性剤濃度
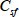
に比例することを示しており,
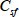
に対して
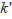
をプロットすることにより,その直線の傾きとミセルの部分比容の値から分配係数を求めることができます。またグラフのx切片は
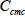
,すなわち泳動条件下での臨界ミセル濃度に相当します。
MEKCの分離は試料物質のミセルへの分配係数の違いに基づくものですから,分解能はクロマトグラフィーの場合と同様に
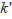
の値に依存することとなります。二成分の
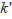
の値がそれぞれ
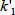
,
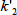
であるとき,これら二成分間の分解能は次式で表されます。
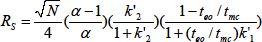
(6・18)
ここで
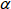
は分離係数であり,
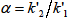
として定義されます。式(6・18)より,理論段数
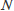
の増加や
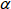
の変化により分解能を向上させることができます。式(6・18)の第四項はMEKCに独特な分解能の
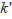
に対する依存性を表しています。この項は,MEKCでは固定相に相当するミセルが移動することに起因する項です。式(6・18)の第三項と第四項との積は次の条件において最大値をとります。
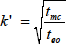
(6・19)
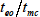
の値は溶出範囲 (elution range) を表す指標で,この値が小さいほど中性分子は広い時間領域で溶出されることになります。通常の条件下ではteo/tmcの値は0.2~0.3程度ですので,式(6・19) から,最適分離を与える
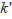
の値は2前後です。
MEKCは,もともと中性分子の分離のために開発された手法ですが,イオン性化合物の分離選択性を変化させるための手法としても優れています。イオン性化合物に対する泳動機構はさらに複雑であり,解離平衡,イオン平衡,ミセルによる解離定数のシフトなどを考慮しなければなりません。

