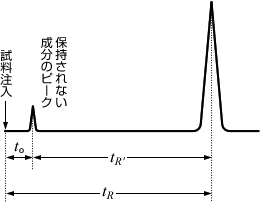
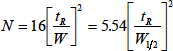試料成分の移動
試料中の成分を分離するには、カラム中で各成分帯が広がらず、重なり合わないことが必要です。図7・2(a)では二成分のピークは完全に分離しています。図7・2(b)では二成分のピーク頂点の間隔は図7・2(a)の場合と同じですが、成分帯が広がって重なり合った結果、ピークは幅が広くて分離不完全です。
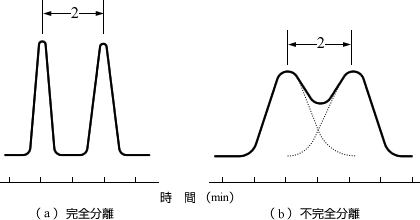
図7・2 二成分の分離例
このように、カラムを溶出してくる成分帯の広がりの大きさによってカラムの分離効率(性能)を判定することができます。そのようなカラム性能を表わす尺度の一つとして理論段数(number of theoretical plates)
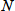
があります。
ここに、
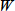
はべ一スラインでのピーク幅、
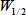
はピーク高さの半分の高さでのピーク幅で半値幅といいます。
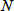
の大きなカラムほど、同じ保持時間のピーク幅は狭くなり、カラム性能が高いことを意味しています。
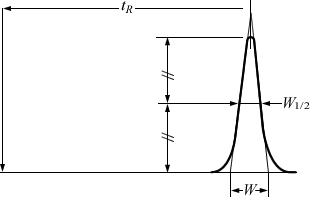
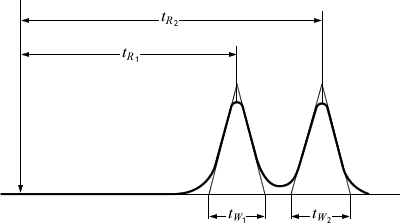
図7・3 理論段数(N) の評価
また、カラム長さ
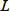
を
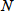
で割った一理論段のカラム軸方向の長さを理論段高さ(height equivalent to a theoretical plate;HETP)
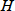
といい、これもカラム性能の尺度となります。
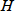
は小さいほどピーク幅は狭くなり、カラム性能が高いことを示します。ところで、
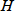
は種々の因子の和として表わされます。移動相に気体を、固定相に液体を用いる気-液クロマトグラフィー(表7・1)では、
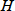
は三つの因子の和として表わされます。
これはvan Deemterの式として知られており、A、B、Cは定数、

は移動相の平均線速度です。第1項は充てん剤粒子の間隙により作られる多くの流路に起因するもので、渦巻拡散項とよばれています。第2項はカラム軸方向での成分の分子拡散に起因する分子拡散項で、第3項は成分分子が移動相と固定相間を移動する際の遅れに起因する物質移動に対する抵抗の項です。
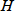
と

の関係を図7・4に示しますが、
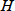
の最小値
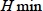
は

が
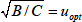
のときとなります。一方、液体クロマトグラフィーでは移動相中での分子拡散
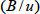
は普通無視できますが、
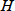
の式はもう少し複雑となります。その式から、粘性の低い移動相を高温でゆっくり流すと
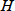
が小さくなることが結論されています。
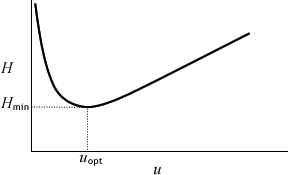
図7・4 van Deemter式のプロット