|
quantum mechanics
古典力学の運動方程式といえばニュートンの運動方程式を思い出すでしょう。これは物体の位置と運動量の時間変化を記述した方程式です。
量子力学ではシュレーディンガー方程式が有名です。これは、ある種の波動方程式です。物体の状態を時間と空間の中での確率振幅(波動関数)として表わし、確率振幅の時空間での変化を記述したのがシュレーディンガー方程式です。
量子力学の形式的な話に到るまでは、私達は主に波(波動関数)を扱います。従って、ここで波に関する基本的な操作を練習し、不確定性関係の理解につなげてゆきます。
まず、色々な波長の波を重ね合わせて、ある場所に局在する波、つまり、波束を作ることを考えましょう。
単純な波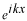 を重ね合わせてみるとどうなるかを調べてみましょう。波長 を重ね合わせてみるとどうなるかを調べてみましょう。波長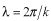 の異なる波を同じ重みで重ね合わせてみます。教科書では重みを の異なる波を同じ重みで重ね合わせてみます。教科書では重みを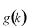 として、 として、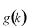 は は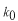 まわりにガウス分布している場合を考えています。ここでは単純に次の様な分布にします。 まわりにガウス分布している場合を考えています。ここでは単純に次の様な分布にします。
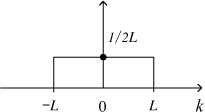 矩形をした分布
重ね合わせの結果、生じる波形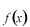 は、 は、
色々な種類の波を重ね合わせるということは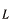 を大きくしていくことに対応します。
を少しずつ大きくしてみて、 を大きくしていくことに対応します。
を少しずつ大きくしてみて、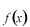 がどのような波形になってゆくかを確かめて下さい。 がどのような波形になってゆくかを確かめて下さい。
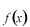 は は =0で山を持ち、 =0で山を持ち、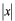 が大きくなると下がっていって、最初に が大きくなると下がっていって、最初に 軸を横切るのは 軸を横切るのは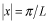 のときです。 のときです。
従って、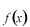 のピークの幅はおよそ のピークの幅はおよそ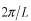 の半分の の半分の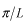 と考えてもよいでしょう。
一方、 と考えてもよいでしょう。
一方、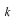 −空間での重ね合わせの重み関数の幅は明らかに −空間での重ね合わせの重み関数の幅は明らかに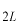 です。 です。
 −空間の幅 −空間の幅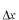 と と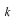 −空間の幅 −空間の幅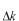 の積を考えてみましょう。 の積を考えてみましょう。
 −空間、 −空間、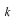 −空間の関数の形によらないで、両空間の関数の幅の積は一定の値になります。 −空間の関数の形によらないで、両空間の関数の幅の積は一定の値になります。
フーリエ変換の関係にある −空間と −空間と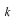 −空間の関数 −空間の関数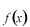 と と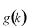 の幅の積は一定値であるという関係があります。
これは数学的な関係ですが、位置と運動量の不確定性関係に結びついていきます。 の幅の積は一定値であるという関係があります。
これは数学的な関係ですが、位置と運動量の不確定性関係に結びついていきます。
|