|
quantum mechanics
2-3. 波の伝播とその方程式
量子力学 - 太田 雅久
単純な波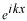 は時間的には は時間的には
のように変化します。この波の位相は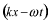 です。時刻 です。時刻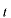 =0で、ある場所 =0で、ある場所
での位相は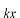 です。時間が です。時間が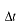 経過すると、 経過すると、 での位相は での位相は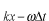 となります。これは時刻 となります。これは時刻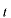 =0で =0で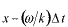 の場所の位相です。 の場所の位相です。 よりも左側(負の方向)にあった位相が時間が経過して よりも左側(負の方向)にあった位相が時間が経過して に到達するので、この波 に到達するので、この波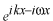 は は の正の方向に進む波になっています。 の正の方向に進む波になっています。
これを真空中の光の波と考えてみましょう。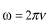 、 、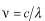 の関係を用いて の関係を用いて
この波を重み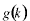 で重ね合わせると、 で重ね合わせると、
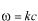 の関係を仮定したため、 の関係を仮定したため、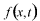 は の速さで伝播してゆく。 は の速さで伝播してゆく。
さらに、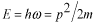 の関係を用いて、 の関係を用いて、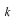 と と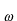 を を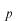 と と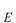 に書替えると、 に書替えると、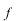 を別の関数 を別の関数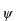 (プサイ)、 (プサイ)、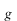 を を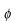 (ファイ)として、 (ファイ)として、
両辺を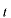 で偏微分し で偏微分し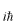 を掛ける。 を掛ける。
この偏微分方程式
は、あとで出てくるシュレーディンガー方程式と同じ形をしてます。
|