図に示されているような
ポテンシャルの階段があるとしましょう。
ポテンシャルが急激に変化する場所が原点にとられています。
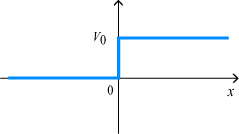
ポテンシャルの階段
エネルギーの尺度は
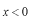
の領域で0にとっています。従って、ポテンシャル・ステップの高さが
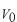
になっています。
まず、簡単な問題として、運動エネルギー
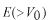
の粒子(質量
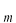
)が
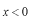
の領域から

の正の方向に進行するとき、
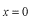
でのポテンシャル変化が、この粒子の運動にどんな影響を与えるのか見てみましょう。つまり、
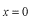
でどれだけ反射して、どれだけ透過するかを計算してみましょう。
この種の問題は、シュレディンガー方程式を境界環境条件のもとに解くことになります。これから出てくる問題はすべてそうです。
計算手順を以下に示します。
(1)ポテンシャルの特徴に応じて領域を分ける。
この場合、
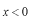
を領域
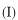
、
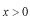
を領域
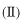
とします。ポテンシャルが複雑になると領域が3つに分かれる場合もあります。
(2)各領域でシュレディンガー方程式を書きます。一般的にシュレディンガー方程式は
です。ここで
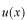
は波動関数といわれるものです。
領域
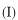
、領域
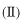
のポテンシャルを代入すると、
(3)これらの方程式を数学的に解きやすい形に変形します。まず、両辺を
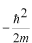
で割って、右辺を左辺に移行します。
次に波数を定義します。
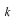
及び
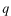
は領域
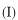
及び領域
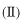
での粒子の波数です。
この次に出てくる束縛問題(エネルギー固有値またはエネルギー順位を求める問題)では境界条件から
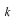
を求めることによって、上に述べた定義から固有値
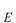
を求めます。しかし、今の問題は
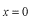
を通過するときの反射と透過を求める散乱問題の一種ですから少し様子が違います。
波数を定義すると方程式は簡素な形になります。
これは前の章で説明した線形二階常微分方程式です。
(4)各領域での
一般解を求めます。
(5)
境界条件を考慮します。この問題では
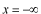
から運動エネルギー
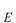
の粒子が

の正の方向に進行してきて、
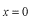
でその一部が反射し、領域
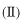
では透過波(

の正の方向に進む波または粒子)のみが存在します。これが境界条件と言われるものです。この条件に適合するように上記の波動関数を書きかえます。
その前に

の正の方向、負の方向に進む粒子を表す波について勉強しておきましょう。
 の正の方向に流束を持つ波 : の正の方向に流束を持つ波 : 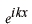
 の負の方向に流束を持つ波 : の負の方向に流束を持つ波 : 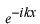
|
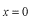
で見た場合、
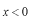
の領域での平面波
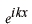
は原点に向かってくると教えられるので内向波といいます。
領域
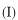
では原点に向かって入射する波と
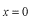
のポテンシャル・ステップで反射されて
負の方向に進む波が重ね合わされています。入射する波の振幅は任意にとってかまいませので、今、
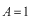
とします。
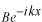
は振幅
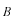
で反射する波です。
また、領域
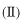
では、ポテンシャル・ステップを通過した波しか存在しません。これは

の正の方向に進む波です。従って、
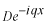
はこの条件に適合しません。
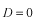
となります。
従って、境界条件を考慮した各領域での波動関数は
となります。ここで、
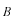
は
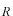
に、
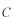
は
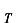
に書きかえられています。より明確に物理的な状況を示す。
意味が書きかえられました。
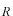
はreflection、
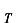
はtransmissionの頭文字です。
(6)
反射係数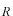
、
透過係数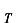
を求めるために
接続条件を用います。2つの領域の境界で波動関数はなめらかでなくてはいけません。つまり、関数値と微係数が等しくなくてはなりません。
先ほどの波動関数をこの条件式に代入しますと、
となり、これらの式から、
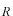
と
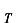
が求まります。
あとは自分で試みてください。