| 5-2 |
| 5-4 |
|
|
|
quantum mechanics
5-3. ポテンシャル井戸での束縛状態
量子力学 - 太田 雅久
図のような深さが有限なポテンシャルの井戸に束縛されている粒子が、どのようなエネルギー状態を取ることができるのかを考えてみます。
このポテンシャルにおけるエネルギー固有値を求める問題です。 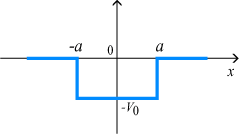 ポテンシャルの井戸 前節と同じ要領で問題にアプローチしましょう。 (1)領域を分ける。 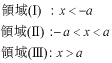 (2)各領域のシュレディンガー方程式を書く。 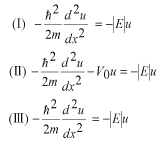 ここで束縛エネルギーは負であるので、 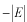 という表し方をしています。また、 という表し方をしています。また、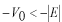 、つまり、 、つまり、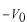 よりエネルギーの高い所にしか状態は現わせません。 よりエネルギーの高い所にしか状態は現わせません。*もちろんのことですが、 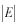 は正ですから、 は正ですから、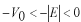 の関係にあります。 の関係にあります。(3)方程式を変形します。 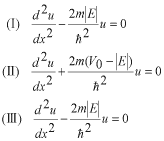 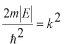 , , 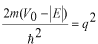 と定義しますと、 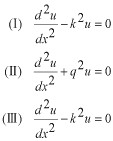 (4)それぞれの一般解は 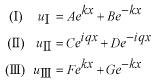 (5)境界条件を考えます。 粒子が束縛されていますから、 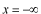 で粒子を見い出す確立は0です。従って、 で粒子を見い出す確立は0です。従って、 において において で で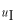 が0となるには、 が0となるには、 でなければなりません。 でなければなりません。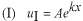 領域  の波動関数はポテンシャルが対称( の波動関数はポテンシャルが対称(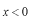 に関して)のため、偶関数と奇関数に分類できます。 に関して)のため、偶関数と奇関数に分類できます。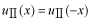 とすると 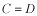 となります。また、 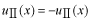 とすると、 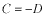 となります。 従って、 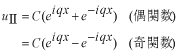 領域  は は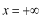 で粒子が存在するはずはありませんので、この条件に適合するには で粒子が存在するはずはありませんので、この条件に適合するには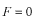 が必要です。 が必要です。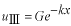 (6)接続条件を用います。 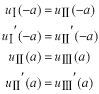 偶関数の場合について考えてみましょう。 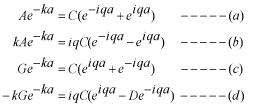 (b)/(a)を実行してみましょう。 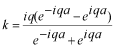 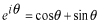 を思い出して、この式を変形します。 を思い出して、この式を変形します。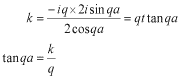 定義から 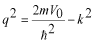 両辺に 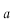 を掛けて を掛けて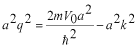 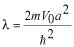 とおくと 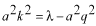 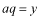 とおいて とおいて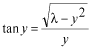 この非線形方程式の解 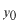 が求まったとすると、 が求まったとすると、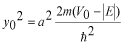 の関係により、 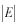 の値が求まります。これが、粒子がこのポテンシャルに束縛された場合にとりうるエネルギーです。 の値が求まります。これが、粒子がこのポテンシャルに束縛された場合にとりうるエネルギーです。解 はこの場合は解析的に解けないので、計算機で数値的に解きます。 奇関数の場合も同様にしてエネルギー固有値を求めるための 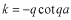 という関係式が得られます。 |
|
|