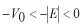
束縛状態の場合はでした。
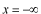
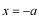
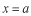
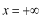
粒子のエネルギーが正の場合は、から平面波がやってきて、で一部が反射し、透過した波数の変化した平面波がで再び一部が反射し、残りがの方向に透過してゆきます。

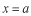
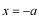
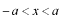
で反射した一部の平面波はの負の方向に進み、で反射と透過が起こります。一般に、の区間では反射と透過が繰り返えされていると考えられます。
この問題を解くのは、束縛状態の場合と同じ手順ですが、シュレディンガー方程式がほんの少し異なります。それぞれの領域で、


また、波数の定義も少し異なってきます。


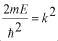
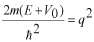
としますと、上記のシュレディンガー方程式は


となって、それぞれの領域での波動関数は次の図を参考にしながら組み立てることができます。


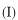
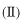
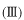
領域には右向きと左向きの平面波が、領域にも同様に右向きと左向きの平面波が、しかし、領域では右向きの平面波だけとなります。
このことから波動関数は、それぞれの領域でのシュレディンガー方程式の一般解を用いて、


となります。
あとは接続条件によって


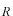
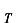
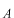
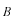
から未知数の,,,を求めることができます。
この計算は少々複雑ですが、講義のときに行います。