今度はデルタ関数形の引力ポテンシャルによる束縛状態を求めることにします。

デルタ関数という、無限に幅の狭いポテンシャルの井戸に束縛状態が発生するのは興味深いことです。量子ドットなどによる電子の束縛を近似的に考えるときに役に立つと思われます。
教科書にあるポテンシャルは


となっています。

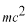
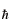
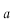
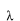
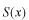
各パラメーターの次元を調べてみましょう。はエネルギーの次元ですので、m[MeV・s2・m-2]の次元を持ちます。は[MeV・s]、は[m]、は無次元としています。従って、はもともと[m-1]の次元を持っていたことになります。

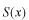
それはの定義より


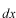
から、右辺が無次元の1になっています。は線素で[m]の次元です。従って、 は[m-1]の次元を持たせています。
この束縛状態を解くのに、今までの(1),(2),・・・の方法を完全にあてはめることはできません。
(1)領域を分ける。


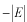
(2)各領域のシュレディンガー方程式は、束縛エネルギーをとすると、二つの領域とも


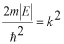
(3)方程式を変形します。と定義して、二つの領域ともに


(4)それぞれの一般解は


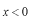
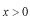
(5)境界条件を考えます。でもでも波動関数は急激に減少してゆかねばなりません。このことを考えにいれますと


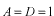
また、ポテンシャルが対称であることを考慮して、としても一般性を失いませんので、結局、


となります。
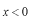
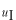
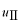
(6)接続条件です。<でのとは同じ値をとりますので連続的です。
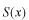
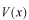
しかし、導関数の傾きが明らかに異なります。この傾きの差を関数ポテンシャルの強さから決定する仕事が最後に残る点です。
完全なシュレディンガー方程式は


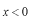
でした。この両辺とを含む非常に微妙な区間


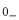
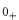
で積分します。 , は次のような意味です。


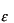
ここでは微妙な変数と考えて下さい。


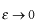
という極限を想定しますので、左辺第二項の積分は積分の下限と上限が近づくのでゼロとなります。
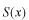
右辺のを含む計算は


を用いるとすぐに計算できます。
結果、


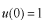
ここでを使っています。
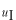
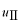
で , の波動関数の微係数を用いて、