 |
|
前節ではp型半導体とn型半導体の接合を考えた。ここでは金属と半導体の接合を考える。例えば金属とn型半導体を接触させると電子の拡散が起き図2−5−1のように空乏層が生じる。この障壁をショットキーバリアといいこの高さ(φb )がショットキーバリアの重要な特性の一つとなる。図2−5−2aのように金属に+の電圧をかけn型半導体に−の電圧をかけると空乏層は狭くなり順方向となる。それに対して図2−5−2bのように逆に電圧をかけると空乏層は広がり逆方向となる。電流電圧特性はpn接合と類似しており
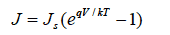 (式4)
となる。(図2−4−2a)ただしここでのJs はpn接合のJ0 とは異なる。また普通はeqV/kT は1よりもかなり大きいので
(式4)
となる。(図2−4−2a)ただしここでのJs はpn接合のJ0 とは異なる。また普通はeqV/kT は1よりもかなり大きいので
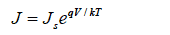 (式5)
と近似できる。Js は
(式5)
と近似できる。Js は
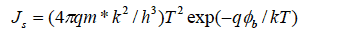 (式6)
でありここでm*は有効質量、φbはショットキーバリアーの高さ(図2−5−1)である。また q は電荷 k はボルツマン定数 h はプランク定数 T は絶対温度である。
(式6)
でありここでm*は有効質量、φbはショットキーバリアーの高さ(図2−5−1)である。また q は電荷 k はボルツマン定数 h はプランク定数 T は絶対温度である。
実際のショットキーバリアーダイオードは(5)式の理論値から多少ずれる。そこで実験値は下記のように表現する。
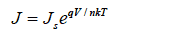 (式7)
ここでnは理想係数といい理論どうりなら n=1 となる。実際のダイオードはものにもよるが市販されているものでも n=1.01〜1.10 程度の値となる。
(式7)
ここでnは理想係数といい理論どうりなら n=1 となる。実際のダイオードはものにもよるが市販されているものでも n=1.01〜1.10 程度の値となる。
実際のショットキーバリアーダイオードは(5)式の理論値から多少ずれる。そこで実験値は下記のように表現する。
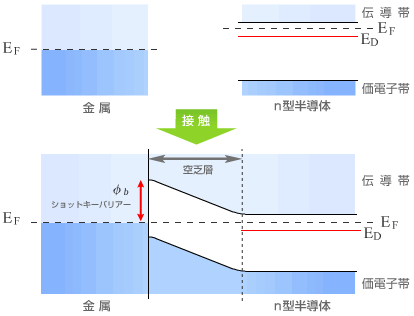 図2−5−1 |
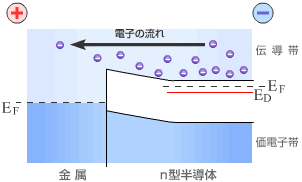 図2−5−2a |
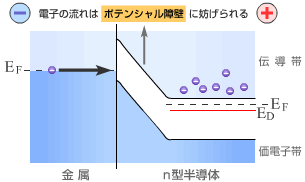 図2−5−2b |
金属と半導体を接触させるとショットキーバリアーが形成される
ショットキーバリアーは整流性を持ちダイオード特性を示す
ショットキーバリアーは整流性を持ちダイオード特性を示す
