 |
光は電磁波の一種で電波と同じ波である。従って光は波長と強度が重要となる。しかし量子論的には電子が波の性質を持つのと同様に光は粒子としての振る舞いをする。この粒子のことを光子またはフォトンと呼ぶ。この様に考えれば光は光子エネルギーと光子数が重要となる。真空中での光の速度cは不変であるからは光の波長をλとすると振動数νはν=c/λとなる。光電効果の実験からプランク定数をhとするとフォトンのエネルギーEはE=hν=hc/λとなる。フォトンのエネルギーは普通eV単位で表される。光の強度はフォトンの数でありフォトンのエネルギーと強度は全く違う意味なので注意する。
半導体に光を照射すると価電子帯の電子は伝導体に励起される。これは一種の光電効果であり(内部光電効果と呼ばれる)量子力学を理解するために非常に重要な現象である。入射フォトンのエネルギーがバンドギャップのエネルギー以下であればなにも起こらない。フォトンのエネルギーがバンドギャップのエネルギー以上であればフォトンのエネルギーは電子を価電子帯から禁制帯をこえ伝導帯に励起するために消耗される。すなわちフォトンは半導体に吸収されその代わりに電子を励起する。(図2−7−1)この実験は光が粒子(フォトン)であることを示す有力な実験である。励起された電子は結晶中を動き回ることができ、半導体の電気伝導度は上昇する。これを光電気伝導という。この光電気伝導を利用して光センサーを作ることが出来る。電気伝導度は吸収されたフォトンの数に比例するがフォトンのエネルギーには比例しない。この光電気伝導を利用して光センサーを作ることが出来る。この実験で使用する半導体のバンドギャップはSiで1.1eV、CdSで2.5eVである。バンドギャップエネルギー以下のエネルギーの光を照射しても電子は励起されない。光の波長がエネルギーに相当し半導体にバンドギャップエネルギーが存在することがことがこの実験から分かる。
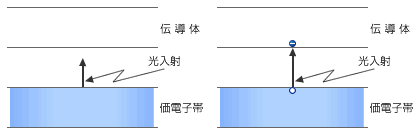 図2−7−1 |
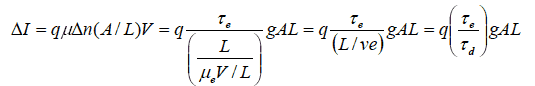 (式12)
(式12)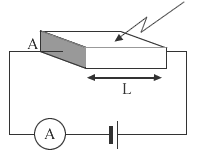 図2−7−2 |
