 |
関連リンク : 太陽電池は地球環境の悪化を抑える一つの有力な材料である。砂漠に太陽電池を敷き詰めれば地球全体の電力需要を賄うことができると言われている。太陽電池を如何に有効に利用するかは、物理学を学び21世紀を生きる我々の一つの課題でもある。そこで太陽電池の特性について少し詳しく述べる。太陽電池はｐｎ接合型ダイオードであるため、図2−3−3のようなIV特性をもつ。これに光を照射すると図2−9−1のようになる。外部に流す電流が0Aの時の電圧を開放端電圧(Voc)と呼び、外部にかかる電圧が0Vの時の電流を短絡電流(Isc)と呼ぶ。これが太陽電池の性能の一つの指標となる。
図2-4-2と図2-8-1を見ればかわるように光電流は順方向とは逆に流れる。従って光電流を JL とすると電圧Vを印加したときに太陽電池に流れる電流は(3)式より
(式14)となる。図2−9−1 で光照射時のIV特性が電流が負の方向にずれているのは(13)式の - JL に相当する。(13)式より短絡電流Iscを求めると V=0 とおけば良く J=-JL となる。また開放端電圧を求めるには J=0 とおけばよく、V=(kT/e)ln(JL/J0+1) となる。
太陽電池は電力を供給するための物であるから図2−9−2のように負荷を与えて使用する。この負荷は電力を消耗するものであり、具体的には照明であったりモーターだったりする。負荷抵抗を変化させたときのI−V特性は図のようになる。抵抗値がゼロの時の電流が短絡電流であり、無限大の時の電圧が開放端電圧(Voc)である。仕事率はW=IVであるから、I−V特性曲線のIとVの積が太陽電池の出力となる。この出力が最大になる電流と電圧の組み合わせを太陽電池の最大動作点と呼び、出力が最大になるように負荷抵抗を選ぶことを整合をとるという。このときに太陽電池の性能が最大限に発揮されることになる。太陽電池を効率よく使うには、うまく整合を取ることが重要である。最大動作点での電圧をVm電流をImとし、入射光の総エネルギーをPintとすると太陽電池の効率はη=Vm Im /Pintと表せる。
太陽電池の接合バンド図（図2−8−1b）を見れば分かるように、一つの太陽電池から得られる電圧には限りがある。バンドギャップエネルギーを電子の電荷で割った電圧（V=eV/e：単結晶シリコンの場合1.1V）以上は原理的に得られない。実際の太陽電池は、複数のセルを直列または並列に接続して一つのモジュールとしている。
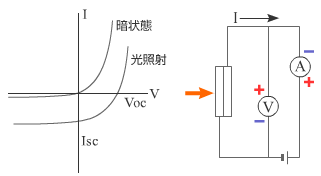 図2−9−1 |
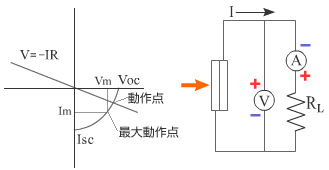 図2−9−2 |
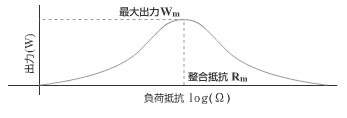 図2−9−3 |
太陽電池の原理を分かり易く水の流れにたとえてみよう。図のような段差のあるダムを考える。短絡電流というのは図のようにダムの左右に水路のバイパスを付けて水を流すことに相当する。水（電子）は左右で自由に流れるために水位（フェルミレベル）は左右で一致する。半導体に光を当て電子を励起すると言うことは水をポンプ（Ｐ）で汲み上げることに相当する。このときには水を汲み上げた分だけ水は流れる。従って光励起した分だけ短絡電流は流れる。
 |
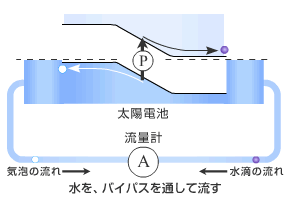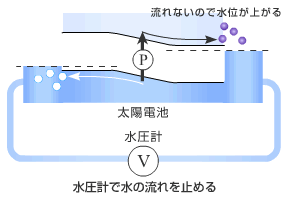
では次ぎに水圧計（電圧計）を挿入しバイパスの水の流れをせき止めてみよう。これは開放端電圧を測定していることに相当する。このときにポンプで水を汲み上げると水は流れないために右側の水位が上がる。このときの左右の水位の差が水圧でありすなわち電圧に相当する。水の流れは高低差を利用しているために汲み上げる量が多くなると高低差が減り水は流れにくくなりあるところで落ちつく。したがってポンプで汲み上げる水の量が多くなってもある程度以上の水圧にはならない。すなわち、入射光量が増加しても開放端電圧はある程度以上にはならない。
 |
入射光子数をいくら増やしても電圧は原理的にある程度以上にはならない。
