次は(2)の問題です。今考えている振動子を、両端が固定された弦に対応させます。両端が固定された長さ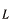の弦の基本振動数は離散的な値をもちます。

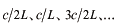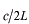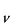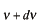離散的な振動数がどのように分布しているのかを調べてみましょう。ですから、一つの基本振動数を次の基本振動数の間隔はです。ということは離散的な振動数の密度は一定になります。このことから、振動数がとの間にある基本振動の数は密度関数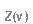を用いて

と表わされます。

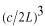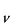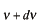我々が問題にしているのは3次元の振動子ですが、同じ考え方を3次元に拡張できます。この場合、離散的な振動数の密度はとなります。振動数がとの間にある基本振動の数は、

ここでは偏光の自由度を考慮して2倍されています。

(1)の結果で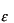を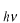で置き換えて、(2)の結果を用いると、体積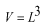を考慮して、単位体積あたりの振動数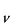と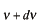の間にあるエネルギー分布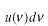が求まります。

振動数の小さい長波長側で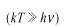、この分布は　Rayleigh−Jeansの公式に近づきます。

また、振動数の大きい短波長側で


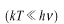
となります。 プランク分布

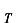
は教科書にも示されているように温度に熱せられた物体から放射される光のスペクトルを見事に説明します。

一つの例として宇宙マイクロ波の背景放射の実測値とこの公式による計算値が示されています。狭い所に超高温状態でとじ込められた光が膨張をはじめ、色々な相互作用によって物質を生み出し、冷却し、現在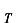＝2．735Kの物体から発する光に相当するものが宇宙に充満していることが示されています。

■理解のポイント
ある物理系のエネルギー平均値を求めるとき、系のもつエネルギー準位が連続的に存在するか（平均値は積分で表されるか）、離散的な値しかとれないか（平均値は無限級数の和で表されるか）によって決定的な違いが生じる

マックスプランクについて 極めて微少なエネルギーを考える場合、エネルギーを連続量として扱えないという考え方は1900年にプランクによって導入され、空洞放射のエネルギースペクトルを見事に説明しました。この考え方は、アインシュタインによって、1905年に光電効果の説明に、また1907年には低温での固体の比熱の説明に用いられました。1908年ラザフォードによってアルファ散乱の実験が行われ、その実験データは1913年のボーアの仮説につながってゆきます。これら一連の流れ、量子力学確立に向けての流れは、1900年のエネルギー量子の導入に端を発していると言えるでしょう。このことより、1918年、プランクにノーベル賞が授与されています。60才でした。